Pascal Implementation by Steven Pemberton and Martin Daniels
This section has to do with the meaning of the program being compiled - the attributes of objects such as the types of variables, the parameters of procedures and so on.
It has four concerns
The key to understanding this section is understanding the types identifier [142-56] and ctp [116] used to represent the attributes of identifiers, and structure [118-32] and stp [116] used to represent the attributes of types.
At each point in a Pascal program as it is being compiled, a number of identifiers are visible for use. Firstly the things declared in the current block. If that block is nested inside another procedure or function then the things declared in that block are visible, and so on out to the outermost level of the program, and then one more level: the standard identifiers of Pascal itself.
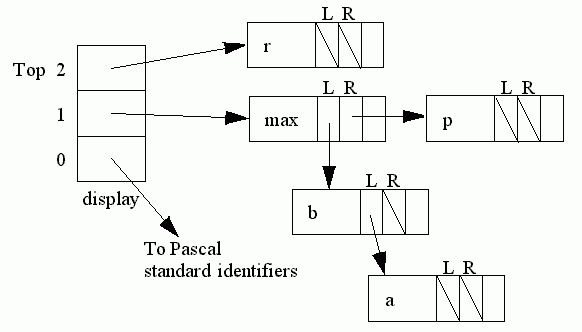
Each nested block is represented by an element in the array called display [250]. Each time a new nested block is entered, a new element is added to display and at the end of the block the element is removed again.
At each level of declaration a tree is formed of the identifiers declared there. The first identifier declared at any level is pointed to by the field fname of the relevant element of the array display [250]. The rlink and llink fields of type identifier then point to lower regions of this tree, rlink pointing to identifiers with alphabetically later names, llink for earlier names. For example with
program eg;
const max=100;
var b, a: real;
procedure p;
var r: real;
begin ... end;
begin ... end.
while the body of procedure p is being compiled, the identifier tree looks like this:

(The variable top always points to the current top element of the display).
These trees are created by the procedure enterid [551-73], which is called while compiling declarations each time a new identifier is declared (for example [1494]). Then every time an identifier is used within the program being compiled, the trees are usually searched using the procedure searchid [588-626], (see for instance [3451]), and occasionally (for forward declared routines, and for field selection) by searchsection [575-86] (on lines [1705] and [2187]).
Searchid works by searching the tree at each level of the display, starting at the top, until the identifier is found, or until the whole structure has been searched without finding it.
This routine enters a declared identifier into the declaration tree at the current level.
[551] Fcp is the pointer to the identifier for this object.
[556] Nam is set to the name of the identifier.
[557] Top is the current level of declaration.
[558-9] If the display is nil then this is the first identifier declared at this level, so display is made to point to it.
[561] Otherwise it must be inserted at the right place in the tree: Lcp will work down the branches of the tree going left or right depending on the alphabetic ordering. Lcp1 will trail one branch behind lcp so that when lcp reaches the bottom (that is, when it becomes nil) lcp1 will point to where the new entry is to be entered. Lleft indicates whether it is to be inserted to the left or right of lcp1.
[562] Save the old value of lcp before going down a branch.
[563-4] If this identifier is already in the tree, then it has already been declared at this level, so error 101 is reported. However, the new identifier is still inserted later on.
[568] If not yet found, go either left or right depending on the alphabetic ordering. Lleft is set to indicate which direction was taken.
[570] Insert the new identifier.
[572] Set the subtrees of the new identifier to nil.
This procedure is called to locate an identifier in the identifier table.
Pascal's scope rules require that first the local declarations be searched, then in the surrounding block, and so on outwards. To effect this, searchid searches each tree in display from top down to 0 until the identifier is found, or it is discovered that the identifier was not declared, in which case a special 'undeclared' entry is returned.
[592] Disx works down through the levels.
[593-605] Search the tree at one level.
[596-604] Fidcls is a set of idclass [137] representing the class of identifier acceptable, for example, variable, type etc. At this point an identifier with the required name has been found. If it is of a suitable class, then this is the required identifier. Otherwise error 103 is reported, and searching continues.
Prterror inhibits the error message during type declarations, when a pointer type may be forward declared (see [1259-60]).
[609] If the identifier was found, goto 1 [596] would have been executed. Thus if the loop terminates normally, the identifier was not found, and so error 104 is issued, and a pointer to a special undeclared entry is returned (these are initialised at [3764-96]).
In this way the caller of searchid can be sure that the result is non-nil, and of an acceptable class.
with lcpl do if name < nam then rlink:=fcp else llink:=fcp
removes the need for lleft. It might be claimed that the existing formulation is more efficient, but this is arguable.
if name > nam then less:=fcp else greater:=fcp;
procedure enterid(fcp: ctp);
var nam: alpha;
procedure enter (var node: ctp);
begin
if node = nil then node:=fcp
else if nodet.name=nam then
begin error(101); enter(node^.less) end
else if node^.name = nam then enter(node^.less)
else enter(node^.greater)
end;
begin nam:=fcp^.name;
enter(display[top].fname);
fcp^.less:=nil; fcp^.greater:=nil
end;
Maxlevel indicates the maximum level of nesting of procedures allowed (see [1747]) and therefore the number of elements in the display with occur = blck. (The compiler itself has a maximum nesting of 8 - procedure factor is at this level).
Displimit is the upper bound of the array display and therefore represents the maximum for the depth of routine nesting plus the number of nested record declarations or nested with statements. It is arguable whether maxlevel is really needed as well as displimit.
Alternatively the display could be organised as a list of elements rather than as an array, which would need no limits at all.
Occasionally only one level of the identifier table is required to be searched:
For these simple cases, procedure searchsection is used. This is very like searchid except that it reports no errors, and it returns nil when it fails to find the identifier.
Since they are so similar, there will be no further discussion of searchsection.
Both searchid and searchsection could be functions returning the ctp.
The other use of identifier trees is to store the fields of a record. When a record type is being declared, top is incremented and the fields of the record entered with enterid. This tree is then stored with the type attributes for the record, and top decremented (see [1329-50], [1130]).
An advantage of this is that when compiling a with statement, the tree for the record can be put on the top of the display, and then identification of identifiers can proceed as usual using searchid (see [3400 et seq.]).
These requirements are the explanation of the occur field of variable display [254]: when an element of the display points to declared variables etc., occur is blck (block); when it points to fields while a record is being compiled it is rec; during a with statement it is crec (constant record) if the record can be directly accessed at runtime (for example a record variable), or vrec (variable record) if it must be indirectly accessed (for example, a pointer to a record).
This field points to the representation of a type (a structure). For variables, constants, and fields it represents the type of that object, for functions it represents the result type. For procedures it is always nil, and for types it holds the representation of that type.
This field has several uses:
To link together forward declared pointers, to be resolved later [1265]. For example, in
type intlist = ^intnode; reallist = ^realnode; intnode = record ival: integer, next: intlist end; realnode = record rval: real; next: reallist end;
Intnode and realnode will be linked by the next field until they are resolved by their declarations.
var a, b: integer;
the idtype for a and b is not known until the integer is reached and this must be filled-in in retrospect.
This indicates whether this identifier is a variable, constant, field, procedure, function, or type.
Procedures and functions may either be standard or declared. In the standard case, key indicates which it is (in order: get, put, reset, rewrite, read, write, pack, unpack, new, release, readln, writeln, mark for procedures, and abs, sqr, trunc, odd, ord, chr, pred, succ, eof for functions, set up in entstdnames [3669-762]). For the declared case, representing routines declared in the program, pflev is the level the routine was declared at, and pfname the label number of its first instruction.
Pfkind is formal for procedures and functions that are parameters of other routines, and actual for normally declared routines.
Formal routines are not implemented in this compiler, and so will not get discussed in great detail. Forwdecl is true for a routine that is forward declared, and extern is true for the standard functions sin, cos, exp, sqrt, ln, and arctan.
Rather than key for standard routines being a subrange of integer, it would be better, safer, and more obvious to make it an enumeration:
type stdroutine= (stdget, stdput, stdreset, ...);
In the variant fields for identifier, we have added empty parts for types and formal to make them explicit:
types: ( ) formal: ( )
Labels are arranged as a list of labels (lbp and labl [183-6]) for each block, accessible from the display starting from flabel (first label) [253].
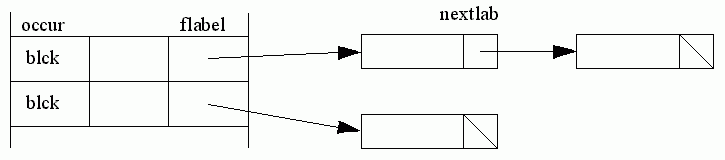
Each label has a field labval, which is the name used in the program, a field labname, the internal name used by the compiler, generated by genlabel, and a field defined, set to true when the label has been used to label a statement. Labels are set up in labeldeclaration [1387-1415].
Types are represented internally by the type structure [118-32].
All types use the size field, which contains the runtime store-size needed to hold an object of that type. (The marked field is used only by the procedure printtables [676-845] when printing out the compiler tables, if the t option is switched on.)
All other fields depend on the form of the type, if it is a pointer, or an array, and so on.
A scalar type is either declared, that is, an enumeration, in which case fconst points to the last identifier in the list (they are linked together by their next field) [1061]; or it is standard, when the type is integer, real, or char (boolean is declared). These latter four can be distinguished by comparing the pointer value to the structure with one of the four pointers intptr, realptr, charptr, boolptr, which are initialised in enterstdtypes [3646 et seq.] (see for example [652-7]).
Here rangetype points to the type of which this is a subrange (for example, integer in 1..10); and min and max hold the minimum and maximum values (1 and 10 in the above case).
Eltype points to the type pointed at (integer in ^integer).
For sets; elset points to the element type of the set (for example, char in set of char).
Inxtype points to the index type of the array and aeltype to the element type, (e.g. char and integer respectively in array[char] of integer).
A multi-dimensional array, like array[1..10, 1..10]of real is treated identically to array[1..10] of array[1..10] of real, so here would give
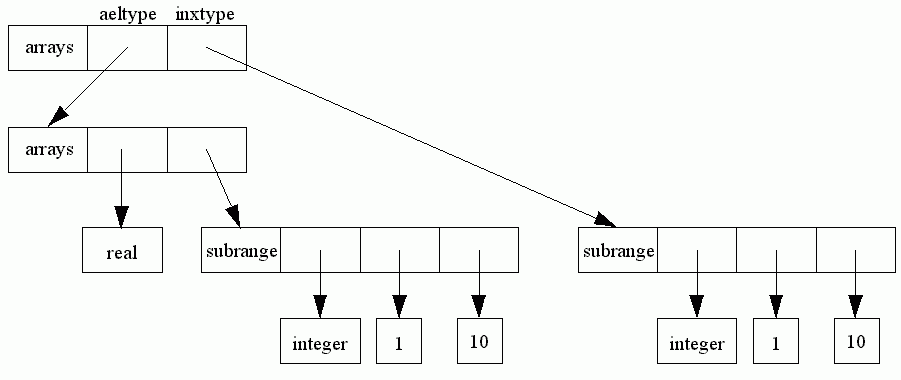
Filtype points to the file type (for example integer in file of integer).
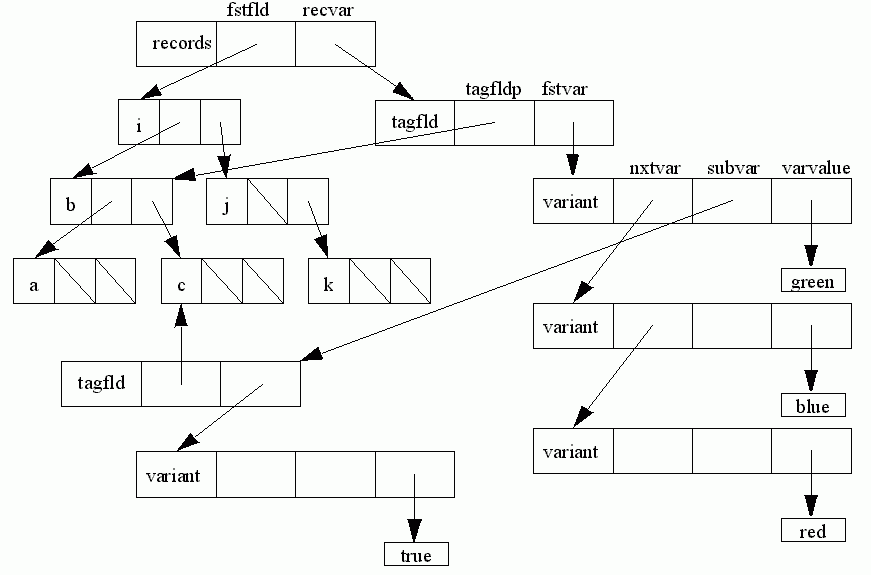
Fstfld points to the first field of the record, the other fields being linked to the binary tree described before.
Recvar points to a structure of form tagfld representing the variant part of the record (it is nil if there is no variant part).
A tagfld has two fields: tagfldp points to the identifier for the tag field, and fstvar points to a list of structures of form variant, each representing one of the case labels.
As an example:
type r= record
i: integer;
case b: colour of
red, blue: (j: integer);
green: (k: integer;
case c: boolean of
true: (a: real)
end;
Types are formed in the procedure typ [1025-1385]. The main semantic routines to do with types are getbounds [628-44], equalbounds [934-44], comptypes [946-1016], and string [1018-23].
The variant part for scalar should have an explicit
standard: ( )
This function is used to decide when two types are compatible.
[951] A type is compatible with itself.
[953] If either type is nil, then an error has been detected earlier, so comptypes returns true [1015] to avoid spurious errors.
[954] With the exception of subranges [1008] two types must have the same form to be compatible.
[956] Integer, real, character, and enumerations.
None of these is compatible with the others. With enumerations, two declarations of the same enumeration are considered to be different types. Scalars are only compatible if fsp1=fsp2 at [951].
[961] Two subranges are considered to be compatible if they are both subranges of the same type.
[963-81] Pointers are the only difficult case:
Globtestp is a pointer to a list of pairs of types, representing pairs of pointers which during this call of comptypes may be compatible, but have yet to be resolved. It is initially empty [3807]. When comptypes is called with a pair of pointers, globtestp is examined to see if it contains this pair [966-72]. If so, it is assumed that they are compatible. Otherwise, they are added to globtestp [974-80], and comptypes called with the element types of the pointers.
This arrangement prevents an infinite loop occurring. Consider the two following types:
lista= record a: char; nexta: ^lista end; listb= record b: char; nextb: ^listb end;
If the two fields nexta and nextb were to be compared for type compatibility, lista and listb would be saved, and then tested for type compatibility.
The a and b fields would be found compatible, and then the nexta and nextb fields tested again. Obviously, if there were no way of stopping at this point, there would be an infinite loop. However, it is found that lista and listb have been saved as a pair - that is that they are already in the process of being compared, and so it is assumed that they are compatible.
In the case of
listc= record c: integer; nextc: ^listc end; listd= record d: char; nextd: ^listd end;
although listc and listd will be saved and therefore assumed to be compatible at one stage, the c and d fields will be incompatible and so at the outer level listc and listd will be incompatible.
Note that at [983] the pair most recently added is removed.
[986] Sets are compatible if their element types are.
[987-93] Arrays are compatible if their index types and element types are, if their run-time sizes are equal, and their indexes have the same values.
[994-1004] Records are compatible if they have the same number of fields [1000], the respective fields are compatible [996-9], and neither has a variant part [1001].
[1006] Files are compatible if their element types are.
[1009-14] If the forms are not equal, but one is a subrange, then the two are compatible if one is a subrange of the other.
if compatible (a, b)
is easier to read than
if comptypes(a, b)
Note that the identifiers of fields play no part in compatibility. Therefore the following two are compatible:
record first integer; last: real end; record last: integer; max: real end;
It is stated in (Amman, 1981) that this is an example of user-friendliness:
a:=b
is allowed because so is
a.first := b.last; a.last := b.max.
However,
var c: record i, j: integer end;
d: record r, s: real end;
d:=c
is not allowed even though the equivalent assignments are:
d.r:=c.i; d.s:=c.j
Are the following pairs of types compatible?
You may find the answer to the last one surprising.
Returns the upper and lower bounds of a subrange type, enumeration type (when the lower bound is always zero), or type char.
The only part that is not immediately obvious is [642-3]. This is for enumerations: fmin is zero already, fmax is obtained from the type.
This routine is clearly in the wrong place. It should be directly before equalbounds [934].
Convince yourself that what is claimed in [630] is true.
This routine is self evident.
Decides if a type is an array of char. Line [1022] could read
string:=comptypes(fsp^.aeltype, charptr)
As an expression is compiled, information regarding it, its 'attributes' such as its type, are stored in the variable gattr [276] of type attr [167]:
attrkind=(cst, varbl, expr);
vaccess=(drct, indrct, inxd);
attr= record typtr: stp;
case kind: attrkind of
cst: (cval: valu);
varbl: (case access: vaccess of
drct: (vlevel: levrange; dplmt: addrange);
indrct: (idplmt: addrange))
end;
An expression can be simple -- a constant or variable -- or it can be more complicated. A variable can be accessed either directly or indirectly.
The field typtr points to the structure representing the expression's type.
The field kind indicates the kind of expression, the two simple cases being a constant, cst, when the value of the constant is pointed to by cval, and a variable, varbl; all other cases (e.g. with operators, variables as values, function calls etc.) are of kind expr.
Variables are split into two subcases: direct and indirect (drct and indrct). Inxd (probably 'indexed') never occurs.
Direct variable expressions result from 'actual' variables [2094] (that is, variables that are not variable parameters, and value parameters), accessing fields of records of records that are themselves direct [2104], function identifiers when the function is being assigned to (for example gcd := x) [2121], and files, like input [2585].
Indirect expressions result from an address being loaded [2031], variable parameters [2099], accessing the fields of indirect records [2111], accessing array elements [2163], and accessing via pointers [2214].
An expression consisting just of a constant: 123
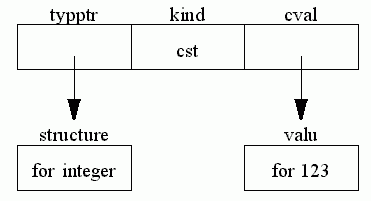
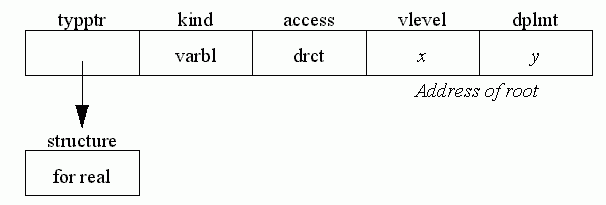
An expression consisting of a variable declared var root: real
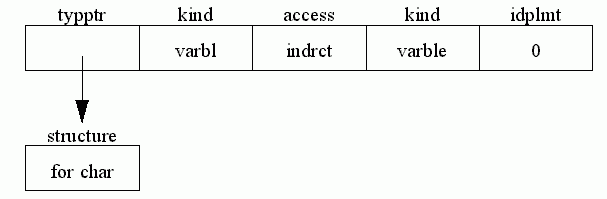
An indirect variable, for example, ch in procedure p(var ch:char);
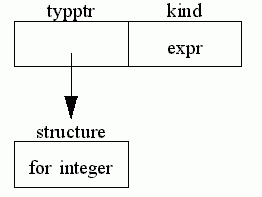
A more complex expression for example i + 1
The fields vlevel and dplmt give the address of a direct variable (its textual level and displacement within that level). These are explained more fully in the chapter on code generation.
The field idplmt gives an offset against the current address loaded on the stack. This is only non-zero for fields of indirect records, where it is the displacement of the required field within the record. This is also explained in the code-generation chapter.
The fact that there are no variant fields for expr and inxd should be made explicit by including
expr: ( )
and
inxd: ()
IXA instructions until
it was known how the element was to be accessed. Of course, another
possibility is that the compiler once did optimise array accessing,
and this was removed.Pascal Implementation by Steven Pemberton and Martin Daniels
Copyright © 1982, 2002 Steven Pemberton and Martin Daniels, all rights reserved.