Der Elementtyp eines Arrays ist in Pascal beliebig. Deshalb kann insbesondere auch ein Array aus Arrays gebildet werden:
PROGRAM MATRIX(INPUT, OUTPUT);
CONST N=3; M=4;
VAR X: ARRAY [1..N] OF
ARRAY [1..M] OF INTEGER;
I,J : INTEGER;
BEGIN
FOR I:= 1 TO N DO
FOR J:= 1 TO M DO
X[I,J]:= I * 4 + J - 4;
FOR I:= 1 TO N DO
BEGIN
FOR J:= 1 TO M DO WRITE(X[I,J]:5);
WRITELN
END;
END.
Bild 28: Programm MATRIX
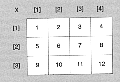
Eine solche zweidimensionale Datenstruktur bezeichnet man in der Mathematik als eine Matrix. Man kann sich die Variable X als eine zweidimensionale Tabelle mit ganzen Zahlen vorstellen:
Bild 29: Matrix X
Üblicherweise wird die obige Deklaration eines mehrdimensionalen Arrays folgendermaßen abgekürzt:
VAR X: ARRAY[1..N, 1..M] OF INTEGER;
Wie Sie im Beispielprogramm sehen, spricht man Elemente einer solchen Struktur durch zwei Indizes an:
X[1,2] := X[2,1] oder ausführlich X[1] [2] := X[2] [1]
In der ausführlichen Schreibweise (die in der Praxis nur sehr selten anzutreffen ist) wird die schrittweise Indizierung besonders deutlich: Zunächst wird eines der Arrays 1 bis N gewählt. In dem so spezifizierten Array erfolgt dann wieder ein indizierter Zugriff auf eines der Elemente von 1 bis M. Dieses Element enthält schließlich einen Wert vom Typ INTEGER.
Es ist eine reine Konvention, bei solchen Matrizen den ersten Index als Zeile und den zweiten Index als Spalte zu bezeichnen. Diese Namensgebung orientiert sich nur an der in der Mathematik üblichen Darstellung von Matrizen, wie sie auch in Bild 29 verwen- det wurde.
Am Beispiel der Ein- und Ausgabe von Matrizen können Sie Ihre Kenntnisse über die Standardprozeduren READ und WRITE wieder auf- frischen. In Bild 28 wurde die Matrix zeilen- und spaltenweise ausgegeben. Diese Formatierung wurde erreicht, indem nach dem Ende der Ausgabe jeder Zeile (innere For-Anweisung) mit WRITELN ein Zeilenvorschub erzeugt wurde.
Möchte man eine Matrix über die Tastatur zeilenweise einlesen, so kann man analog die Prozeduren READ und READLN verwenden. Gibt der Benutzer die Elemente in folgendem Format ein,
1 2 3 4 5 6 7 8 9 10 11 12
soll gelten: X[1,2] = 2 und X[3,1] = 9. Daher benutzt man wiederum zwei geschachtelte For-Anweisungen. Eine Laufvariable (i) indiziert die Zeilen, die andere (j) durchläuft in jeder Zeile die Spalten.
FOR I:= 1 TO N DO
BEGIN
FOR J:= 1 TO M DO
READ(X[I,J]);
READLN; (* ignoriere den Rest der Zeile *)
END
Die Prozedur READLN sorgt also dafür, daß die Eingabe korrekt in verschiedenen Zeilen erfolgt. Um Mißverständnissen vorzubeugen zeigt das nächste Programm, wie die gleiche Matrix auch transponiert gedruckt werden kann. Das bedeutet, daß in jeder Ausgabezeile Elemente mit dem gleichen 2. Index erscheinen. Es genügt also, die innere mit der äußeren For-Anweisung gegenüber Bild 28 zu vertauschen:
FOR J:= 1 TO M DO
BEGIN
FOR I:= 1 TO N DO
WRITE(X[I,J]:5);
WRITELN;
END
Ausgabe:
1 5 9 2 6 10 3 7 11 4 8 12
In der Mathematik existieren zahllose Anwendungen für Matrizen mit reellen oder ganzzahligen Koeffizienten. Die mathematischen Algorithmen besitzen meist sehr übersichtliche Formulierungen in Pascal, jedoch ist im Rahmen dieses Buches eine Besprechung des theoretischen Hintergrundes nicht möglich. Auf der beiliegenden Diskette findet sich ein Programm (NEWTON.P), das eine Matrix durch ein Iterationsverfahren invertiert. Das folgende Programm verwendet ebenfalls Verfahren aus der Mathematik, jedoch sind die zugrundeliegenden Überlegungen etwas einfacher darzustellen.
PROGRAM FAHRPLAN (INPUT, OUTPUT);
CONST STATIONEN = 4;
VAR VERBINDUNG, VERBINDUNG0, VERBINDUNGNEU
: ARRAY [1..STATIONEN, 1..STATIONEN] OF BOOLEAN;
VON,NACH,UEBER: INTEGER;
UMSTEIGEN : INTEGER;
WEG : BOOLEAN;
CH : CHAR;
BEGIN
WRITELN('GEBEN SIE DIE VERBINDUNGEN ZWISCHEN DEN');
WRITELN(STATIONEN,'*',STATIONEN,' STATIONEN IN');
WRITELN('FOLGENDEM FORMAT EIN:');
WRITELN(' + - + -');
WRITELN(' + + + -');
WRITELN(' - - - +');
WRITELN(' - + + +');
(* DIREKTE VERBINDUNGEN EINLESEN: *)
FOR VON:= 1 TO STATIONEN DO
BEGIN
FOR NACH:= 1 TO STATIONEN DO
BEGIN
REPEAT (* '+' oder '-' lesen *)
READ(CH);
UNTIL (CH ='+') OR (CH='-');
VERBINDUNG0[VON, NACH]:= CH = '+';
END;
READLN;
END;
VERBINDUNG:= VERBINDUNG0;
FOR UMSTEIGEN:= 0 TO STATIONEN DO
BEGIN
WRITELN(' VERBINDUNGEN MIT 0-', UMSTEIGEN,
'-MAL UMSTEIGEN:');
(* ZEIGE VERBINDUNGEN FORMATIERT AN: *)
FOR VON:= 1 TO STATIONEN DO
BEGIN
FOR NACH:= 1 TO STATIONEN DO
IF VERBINDUNG[VON,NACH] THEN
WRITE('+':3)
ELSE
WRITE('-':3);
WRITELN;
END;
WRITELN;
(* NEUE VERBINDUNGEN BERECHNEN: *)
FOR VON:= 1 TO STATIONEN DO
FOR NACH:= 1 TO STATIONEN DO
BEGIN
WEG:= FALSE;
FOR UEBER:= 1 TO STATIONEN DO
WEG:= WEG OR
VERBINDUNG[VON,UEBER] AND
VERBINDUNG0[UEBER,NACH];
VERBINDUNGNEU[VON,NACH]:= WEG;
END;
VERBINDUNG:= VERBINDUNGNEU;
END; (* FOR UMSTEIGEN *)
END.
Bild 30: Verbindungen bestimmen
Das Programm löst folgendes Problem: Gegeben sind vier Stationen (z.B. Bahnhöfe in Frankfurt, München, Hamburg und Berlin). Zwischen manchen Stationen existieren direkte (Zug-) Verbindungen, zwischen anderen jedoch nicht. Außerdem ist es möglich, daß zwar eine Direktverbindung von Frankfurt nach München existiert, jedoch nicht umgekehrt.
Mit der Kenntnis über die Direktverbindungen soll das Programm nun die Verbindungen berechnen, die sich durch Umsteigen ergeben: Angenommen es existierte eine Verbindung von Hamburg nach Frankfurt und von dort eine Verbindung nach München. Mit einmaligem Umsteigen in Frankfurt kann man dann von Hamburg aus München erreichen, auch wenn zuvor keine Verbindung existierte. Läßt man mehrmaliges Umsteigen zu, so entstehen eventuell weitere Verbindungen, die das Programm ebenfalls anzeigen soll.
Der erste Schritt zur Lösung einer Aufgabe in Pascal besteht meist in der Bestimmung der Datenstruktur zur Speicherung der Informationen. Wie in diesem Abschnitt nicht anders zu erwarten ist, handelt es sich hierbei um eine Matrix (in der Mathematik unter dem Gattungsnamen Adjazenzmatrix bekannt). Die Verbindungsmöglichkeiten lassen sich z.B. tabellarisch folgendermaßen darstellen:
| VON/NACH | Franfurt | München | Hamburg | Berlin |
| Frankfurt | ja | ja | ja | nein |
| München | nein | ja | nein | nein |
| Hamburg | ja | nein | ja | ja |
| Berlin | ja | nein | ja | ja |
Deshalb wurde die Variable VERBINDUNG folgendermaßen deklariert:
VERBINDUNG: ARRAY [1..STATIONEN, 1..STATIONEN] OF BOOLEAN;
Numeriert man die Stationen in der obigen Reihenfolge von 1 bis 4 durch, so gilt also:
VERBINDUNG [1,1] = TRUE VERBINDUNG [1,2] = TRUE VERBINDUNG [1,3] = TRUE VERBINDUNG [1,4] = FALSE
Generell gilt VERBINDUNG[VON, NACH] = TRUE genau dann, wenn eine Verbindung von Station VON nach Station BIS existiert. Zur einfachen Ein- und Ausgabe wird eine existierende Verbindung mit »+« markiert, während eine fehlende Verbindung mit »-« markiert wird. Damit läßt sich obige Tabelle kompakt schreiben als:
+ + + - - + - - + - + + + - + +
Die Ein- und Ausgabe erfolgt wieder zeilenweise nach dem bereits bekannten Schema durch zwei geschachtelte For-Anweisungen. Offensichtlich wird die Lesbarkeit eines Programmes stark durch die Verwendung aussagekräftiger Variablennamen (VON, BIS, VERBINDUNG) erhöht.
Bevor Sie sich zu sehr mit den Details des Programmes belasten, sollten Sie folgende Struktur des Algorithmus erkennen:
codierte Matrix der Verbindungen einlesen Für 0 bis 4 Umsteigemöglichkeiten Zeige Matrix der Verbindungen codiert an Berechne neue Verbindungsmatrix unter Berücksichtigung der durch ein zusätzliches Umsteigen entstehenden Verbindungen. Übernehme die neue Matrix als Arbeitsmatrix
Wie bestimmt man aber aus dem Inhalt der Matrix VERBINDUNG die Matrix VERBINDUNGNEU? Dazu bestimmt man für jedes Paar von Ausgangs- und Zielstation (VON und BIS) jeden Weg, der über eine beliebige Zwischenstation UEBER führt: Für VON = Hamburg und BIS = München erhält man z.B. folgende Regel:
Es existiert genau dann ein Weg (evtl. mit einmaligem Umsteigen) von Hamburg nach München, wenn eines der folgenden Verbindungspaare existiert:
von Hamburg über Frankfurt nach München ODER von Hamburg über München nach München ODER von Hamburg über Hamburg nach München ODER von Hamburg über Berlin nach München
Diese Berechnungsregel wird durch die innerste For-Anweisung realisiert:
WEG:= FALSE;
FOR UEBER:= 1 TO STATIONEN DO
WEG:= WEG OR
VERBINDUNG[VON,UEBER] AND VERBINDUNG0[UEBER,NACH];
VERBINDUNGNEU[VON,NACH]:= WEG;
Indem man diese Regel nacheinander für alle Paare VON,BIS wiederholt, erhält man eine neue Matrix VERBINDUNGNEU. Wiederholt man diese Berechnung (Schleife FOR UMSTEIGEN:= ...), so erhält man auch Verbindungen mit mehrmaligem Umsteigen.
In einem weniger ausgebauten Schienennetz könnte man also folgende Folge von Matrizen erhalten:
Verbindungen mit 0-0-mal Umsteigen:
+ + - - - + + - - - + + + - - +
Verbindungen mit 0-1-mal Umsteigen:
+ + + - - + + + - - + + + + - +
Verbindungen mit 0-2-mal Umsteigen:
+ + + + + + + + + + + + + + + +
In dem Programm aus Bild 30 findet sich auch die Zuweisung VERBINDUNG:= VERBINDUNGNEU. Mit ihr werden alle 16 Elemente der Matrix VERBINDUNGNEU in die Matrix VERBINDUNG kopiert. Solche Blockzuweisungen sind in Pascal bei jedem zusammengesetzten Typ möglich. Bei mehrdimensionalen Arrays können dabei hierarchisch Teile der Struktur kopiert werden. Man gibt dazu beim Variablennamen jeweils die Indizes nur bis zu der Dimension an, die komplett verändert werden soll:
VAR H1, H2: ARRAY [0..20] OF
ARRAY [1..4] OF
ARRAY [1..10] OF INTEGER;
Mit etwas Phantasie kann man in dieser Datenstruktur zwei Hochhäuser mit 20 Stockwerken (einschließlich Erdgeschoß) erkennen. In jedem Stockwerk gibt es vier Flure. Jeder Flur besitzt die Zimmernummern 1 bis 10. Für jedes Zimmer wird schließlich die Anzahl der Personen (vom Typ INTEGER) gespeichert. H1 und H2 sind also dreidimensional. Mit folgenden Zuweisungen kann man einige Umzüge durchführen:
H1[1,2,2]:= H1[1,2,3]; H1[1,2,3]:= 0
Hier zieht also eine Familie (?) aus dem 1. Stock 2. Flur in die Nachbarwohnung um. Die verlassene Wohnung bleibt leer. Wenn alle Bewohner des 3. Flurs im 2. Stock die Wohnungen mit den gleichen Zimmernummern im 4. Flur im Erdgeschoß übernehmen sollen, wird das in der Zimmerbuchführung so notiert:
H1[0,4]:= H1[2,3] entspricht der Schleife FOR ZIMMER:= 1 TO 10 DO H1[0,4,ZIMMER]:= H1[2,3,ZIMMER]
Beim Umzug des kompletten 1. Stockwerks in das 2. Stockwerk genügt folgende Zuweisung:
H1[2]:= H1[1] entspricht der Schleife
FOR FLUR:= 1 TO 4 DO
FOR ZIMMER:= 1 TO 10 DO
H1[2,FLUR,ZIMMER]:= H1[1,FLUR,ZIMMER]
Größere Unruhe in beiden Hochhäusern wird wohl die folgende Aktion zur Folge haben:
H1:= H2 entspricht der Schleife
FOR STOCK := 0 TO 20 DO
FOR FLUR := 1 TO 4 DO
FOR ZIMMER:= 1 TO 10 DO
H1[STOCK,FLUR,ZIMMER]:= H2[STOCK,FLUR,ZIMMER]
1. Schreiben Sie ein Programm, das in einem aufsteigend sortierten Array A ganzer Zahlen nach einer vorgegebenen Zahl W sucht. Dabei soll die Methode der binären Suche verwendet werden: Um im Teilarray von L bis R das Element W zu finden, vergleicht man W mit dem Wert an der mittleren Position M=(L+R) DIV 2. Je nachdem, ob W kleiner oder größer als A[M] ist, wählt man M als neue linke oder rechte Arraygrenze.
PROGRAM BINARYSEARCH (INPUT,OUTPUT);
CONST UG = 0; OG = 40;
VAR A: ARRAY [UG..OG] OF INTEGER;
W: INTEGER;
M,L,R: INTEGER;
BEGIN
(* Array A zufällig sortiert (!) belegen: *)
W:= 0;
FOR M:= UG TO OG DO
BEGIN
W:= W + INT(RANDOM(0) * 12);
A[M]:= W; WRITE(W:4);
END;
WRITELN;
WRITE('Suche nach:'); READLN(W);
L:= UG; R:= OG;
REPEAT
M:= (L+R) DIV 2;
IF W<A[M] THEN ... ELSE
IF W>A[M] THEN ...
ELSE ...
UNTIL ...
IF ... THEN
WRITELN('gefunden!')
ELSE
WRITELN('nicht gefunden!');
END.
Sollten Sie Probleme bei der Formulierung des Abbruchkriteriums haben, können Sie eine boolesche Variable GEFUNDEN verwenden. Wenn Sie schon Programmiererfahrung besitzen, sollten Sie versuchen, in der Repeat-Schleife mit nur einem Vergleich zwischen W und A[M] auszukommen. (Es geht!).
2. Schreiben Sie ein Programm, das das Pascalsche Dreieck druckt. Es enthält die Binomialkoeffizienten n über k, die man z.B. zur Berechnung von (a + b)^n benötigt:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
... ... ... ... ... ... ...
Dabei steht in der n. Zeile an der k. Position die Summe der Zahlen in der n-1. Zeile an der k-1. und k. Position. Genaueres finden Sie in jedem Lexikon.
3. Schreiben Sie ein Programm, das ein Array reeller Zahlen (z.B. Funktionswerte) verwaltet. Zu Anfang ist das Array unbelegt. Dann sollen Werte vom Benutzer eingegeben werden, die direkt bei der Eingabe so in das Array eingefügt werden, daß die Zahlen aufsteigend sortiert bleiben.
Das Programm hat also folgende Grobstruktur:
LEN:= 0; REPEAT Zahl einlesen; Zahl in Array an korrekter Position einfügen; LEN:= LEN+1 UNTIL LEN = Feldgröße
4. Schreiben Sie ein Programm, das einen Text zeilenweise von der Tastatur einliest. Dieser Text soll dann im Blocksatz auf eine vom Benutzer wählbare Spaltenbreite von N Zeichen verteilt ausgedruckt werden.
Dies ist ein Beispiel für den Blocksatz mit wenigen Spalten.
Sie müssen also zunächst eine Verteilung der Wörter über die Zeilen vornehmen, dazu müssen Sie sich an den Wortzwischenräumen (' ') orientieren. Anschließend müssen Sie jede Zeile auf die geforderte Länge von N Zeichen auffüllen, indem Sie zusätzliche Leerzeichen gleichmäßig zwischen den Wörtern einfügen.
Verwenden Sie zur Speicherung des Textes ein Array von Strings. Sicher können Sie die Funktionen LENGTH, POS, INSERT in diesem Zusammenhang gut verwenden.
5. Schreiben Sie ein Programm, das eine reelle Zahl X gemäß der deutschen Konventionen mit Komma und Trennzeichen druckt. Dabei sollen insgesamt N Zeichen gedruckt werden und M soll die Anzahl der Nachkommastellen definieren.
X:= 12.34 N=10 M=2 _____12,34 X:=1E+7 N=20 M=2 _______10.000.000,00 X:=-0.07 N=10 M=4 ___-0,0700 X:=9.876 N=10 M=0 _________9
Wie bei Aufgabe 4 können Sie sich Ihre Aufgabe durch die geschickte Verwendung der vordefinierten Stringprozeduren (STR, POS, INSERT, CONCAT) stark vereinfachen.
6.Erstellen Sie ein Program, das einen String S1 in einem String S2 sucht. Die gefundene Position soll in der Variablen M gespeichert werden. Im Gegensatz zur Funktion POS darf S1 auch sogenannte Joker enthalten:
S1:= 'Dies ist ein Testtext'; S2:= 'tt'--> M= 17 S2:= 'Tes??e'--> M= 14 S3:= 'ein?T' --> M= 10 S3:= 'Egon' --> M= 0
7.Für eine vom Benutzer eingegebene Matrix mit drei Zeilen und vier Spalten wie z.B.
10 20 30 40 40 30 20 10 11 12 13 -5
sollen folgende Werte berechnet werden:
Natürlich werden Sie dafür For-Anweisungen verwenden und die Größe der Matrix durch Konstanten (N=3, M=4), die Sie auch bei den For-Anweisungen benutzen, veränderbar gestalten!
8. Programmieren Sie das Sortierverfahren Bubblesort. Um ein Array von N Werten zu sortieren, wird das Array (N-1) mal durchlaufen. In jedem Durchlauf werden jeweils zwei benachbarte Elemente vergleichen und ausgetauscht, falls das zweite Element kleiner als das erste Element ist.
PROGRAM BUBBLESORT (INPUT,OUTPUT);
CONST N = 8;
VAR A: ARRAY[1..N] OF INTEGER;
I,J,H: INTEGER;
BEGIN
FOR I:= 1 TO N DO A[I]:= INT(RANDOM(0)*100);
FOR I:= 2 TO N DO
FOR J:= .............. DO
IF A[J+1] < A[J] THEN
BEGIN (* vertauschen *)
H:= A[J]; A[J]:= A[J+1]; A[J+1]:=H
END;
WRITELN('Sortierte Folge:');
FOR I:= 1 TO N DO WRITE(A[I]:4);
WRITELN;
END.
Bestimmen Sie die Grenzen für die innere For-Anweisung, indem Sie sich zunächst die Funktionsweise mit der Anweisung FOR J:= 1 TO N-1 klarmachen, und anschließend überlegen, bis zu welcher Grenze das Array im I-ten Durchlauf bereits sortiert ist.
9. Schreiben Sie ein Programm, das eine Rosette wie im folgenden Bild zeichnet:
Bild 31: Eine Rosette
Der Benutzer wählt die Anzahl der Endpunkte N (im Beispiel N=8), die in gleichem Winkelabstand auf einem Kreis liegen sollen (Winkel 360 Grad = 2 * \MS{\pi}). Nachdem Sie die Bildschirmkoordinaten dieser N Punkte berechnet haben, verbinden Sie jeden der Punkte mit allen übrigen Punkten. Vermeiden Sie, daß die Linien doppelt gezeichnet werden oder die Endpunkte mehr als einmal berechnet werden!