Inhaltsverzeichnis

2.9 Die Datenstruktur Array

In der Praxis kommt man mit den bisher besprochenen einfachen Datentypen nicht aus. Will man nämlich auf einer Menge gleichartiger Werte die gleiche Operation wiederholen, so müßte man für jedes Objekt einen eigenen Namen definieren und diese Operation mit jeder Variable einzeln durchführen.

Eine Addition von 100 Gehältern möchte man natürlich nicht als

VAR GEHALT1, GEHALT2, ..., GEHALT100: REAL;
 
SUMME:= GEHALT1 + GEHALT2 + .... + GEHALT100

programmieren. Für solche Probleme vereinbart man - anschaulich gesprochen - eine Tabelle aller Werte. Nur die Tabelle erhält einen Namen, so daß jeder einzelne Wert über den Bezeichner der Tabelle zusammen mit einem Index in der Tabelle angesprochen wird. Einen solchen Datentyp nennt man in Pascal ein Array (Feldvariable).

Die einfachste Form eines Arrays besitzt als Elemente einzelne (skalare) Werte. Dabei spielen Arrays von Zeichen und Strings eine besondere Rolle. Im Abschnitt 2.9.3 werden mehrdimensionale Arrays, also Arrays von Arrays, besprochen.

2.9.1 Eindimensionale Arrays

Zunächst wird ein Beispielprogramm mit Arrays vorgestellt, damit Sie sich eine intuitive Vorstellung von den Anwendungsmöglich- keiten von Array-Variablen machen können:

PROGRAM GEHALTSKONTO (INPUT, OUTPUT);
  CONST N = 8;
  VAR   GEHALT: ARRAY [1..N] OF REAL;
        MAXGEHALT: REAL;
        OPERATION: CHAR;
        I        : INTEGER;
BEGIN
  FOR I:= 1 TO N DO
    GEHALT[I]:= 1000;
  REPEAT
    FOR I:= 1 TO N DO
      WRITE(GEHALT[I] : 6: 2);
      WRITELN;
      WRITELN('+  Gehaltserhöhung');
      WRITELN('-  Gehaltskürzung');
      WRITELN('=  Gehaltsangleich');
      WRITELN('*  Programmende');
      READLN(OPERATION);
      CASE OPERATION OF
      '+': BEGIN
             WRITE('Für Konto :'); READLN(I);
             GEHALT[I]:= GEHALT[I] + 50;
           END;
      '-': BEGIN
             WRITE('Für Konto :'); READLN(I);
             GEHALT[I]:= GEHALT[I] - 50;
           END;
      '=': BEGIN  (* suche maximalen Verdienst *)
             MAXGEHALT:= GEHALT[1];
             FOR I:= 2 TO N DO
               IF GEHALT[I]>MAXGEHALT THEN
                 MAXGEHALT:= GEHALT[I];
             (* Nivelliere Gehälter: *)
             FOR I:= 1 TO N DO
               GEHALT[I]:= MAXGEHALT
           END;
      '*': 
      ELSE WRITE(#7)
    END (* CASE *)
  UNTIL OPERATION = '*';
END.

Das Programm verwaltet eine Tabelle von N = 8 Gehältern. Aus einem Menü kann der Benutzer folgende Operationen wählen:

1. Ein einzelnes Gehalt kann gezielt erhöht werden.
2. Ein einzelnes Gehalt kann gezielt gekürzt werden.
3. Alle Gehälter können an das maximale Gehalt der Tabelle angepaßt werden.

Arrays werden wie alle anderen Variablen im Deklarationsteil aufgeführt. Der Typ Array wird folgendermaßen beschrieben:

ARRAY [Indextyp] OF Elementtyp

Beispiele für die Deklaration von Arrayvariablen sind

CONST MAXINDEX=5;
VAR   A: ARRAY [5..8] OF INTEGER;
      T: ARRAY [0..MAXINDEX] OF REAL;

Der Elementtyp bezeichnet den Typ der im Array gespeicherten Werte. Bei der Gehaltstabelle und dem Array T werden reelle Zahlen gespeichert, während in dem Array A ganze Zahlen gespeichert werden. Schon jetzt können Sie sich merken, daß als Elementtyp jeder Typ der Sprache Pascal zulässig ist.

Um nun gezielt auf die einzelnen Elemente eines Arrays zuzugreifen, besitzt jedes Element einen Index. Durch den Variablennamen, gefolgt von einem Indexausdruck in eckigen Klammern wird ein Element des Arrays indiziert (spezifiziert):

WRITELN(GEHALT[1]);
GEHALT[3]:= 3000.25;
GEHALT[I]:= MAXGEHAHLT;
IF GEHALT[I]>MAXGEHALT THEN MAXGEHALT:= GEHALT[I];

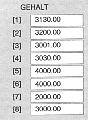
Die Menge der zulässigen Indizes wird bereits bei der Deklaration durch den Indextyp festgelegt. In den Beispielen läßt sich die Variable GEHALT mit den ganzen Zahlen zwischen 0 und N indizieren, während für das Array A nur die Zahlen 5,6,7 und 8 erlaubt sind. Der Indextyp bestimmt also die Größe eines Feldes.

Bild 25: Struktur der Variablen GEHALT

Indizierte Variablen können wie jede andere Variable in Zuweisungen, Ausdrücken und Parameterlisten verwendet werden. Jedoch muß der Typ des Indexausdruckes immer mit dem bei der Deklaration vereinbarten Indextyp übereinstimmen:

GEHALT[3.5]:= 30.0    FALSCH !

Die reelle Konstante 3.5 ist also nicht als Index zulässig. Jedoch kann der Index auch durch eine Variable oder als Ergebnis eines komplexen Ausdruckes definiert werden:

VAR I: INTEGER;
 
GEHALT[I]:= GEHALT[(I+1) MOD N];

Die For-Anweisung wird am häufigsten im Zusammenhang mit Arrrays benutzt. Man läßt die Laufvariable den Indexbereich überstreichen und kann so in einer Schleife eine Operation auf alle Elemente des Arrays anwenden:

PROGRAM ARRAY0 (INPUT,OUTPUT);
  VAR I: INTEGER;
      A: ARRAY[-5..5] OF REAL;
BEGIN
  FOR I:= -5 TO 5 DO
    A[I]:= SQR(SIN(I));
  FOR I:= -5 TO 5 DO
    WRITELN('ELEMENT', I:3, 'ENTHAELT DEN WERT ',A[I]);
END.

In Pascal müssen die Indexgrenzen bei der Deklaration durch Konstanten gegeben sein. Somit muß bereits bei der Übersetzung die endgültige Größe des Arrays festgelegt werden. Um diese Einschränkung etwas zu mildern, definiert man die Indexgrenzen mit Kontanten, die im Konstantenvereinbarungsteil zuvor definiert wurden:

CONST ANZAHLMITARBEITER = 2000;
VAR   GEHALT : ARRAY [1..ANZAHLMITARBEITER] OF REAL;

Natürlich müssen diese Konstanten dann auch im Anweisungsteil z.B. als Grenze für For-Anweisungen benutzt werden. Stellt sich heraus, daß die Grenze zu groß oder zu klein gewählt wurde, muß man nur die Konstante im Vereinbarungsteil anpassen und das Programm neu übersetzen.

In den bisherigen Beispielen wurde als Indextyp immer ein Teilbereich der ganzen Zahlen deklariert. In einzelnen Fällen kann es jedoch auch sinnvoll sein, andere Typen als Indizes zu vereinbaren. Außer dem Typ REAL kann man alle einfachen Typen verwenden:

VAR ZEICHEN: ARRAY [BOOLEAN] OF CHAR;
    ZAHLEN : ARRAY [CHAR] OF INTEGER;
    BUCHSTABEN: ARRAY ['A'..'Z'] OF INTEGER;

Für das letzte Beispiel zeigt Bild 26 noch ein vollständiges Programm. Es wird ein Text von der Tastatur gelesen und die Häufigkeit aller Buchstaben gezählt. Die Texteingabe wird durch die Eingabe eines beliebigen Sonderzeichens beendet:

PROGRAM HAEUFIGKEIT (INPUT, OUTPUT);
  CONST SPACE = ' ';
  VAR   C: CHAR;
        H: ARRAY ['A'..'Z'] OF INTEGER; (* ZAEHLARRAY *)
BEGIN
  (* ALLE ZAEHLER LOESCHEN *)
  FOR C:= 'A' TO 'Z' DO H[C]:= 0;
  READ(C);
  WHILE (C>='A') AND (C<='Z') OR (C=SPACE) DO
    BEGIN
      IF C<>SPACE THEN H[C]:= H[C] + 1;
      READ(C);
    END;
  FOR C:= 'A' TO 'Z' DO
    WRITE(C:2, H[C]:4, '-MAL, ');
  WRITELN;
END.

Bild 26: Buchstabenstatistik

Im Rest dieses Kapitels lernen Sie noch einige typische Operationen auf Arrays kennen. Dabei wird der folgende Deklarationsteil vorausgesetzt:

PROGRAM FELDER (INPUT,OUTPUT);
  CONST UG =  1;    (* untere Grenze *)
        OG = 10;    (* obere Grenze  *)
  VAR   I, J, K     : INTEGER;
        A           : ARRAY [UG..OG] OF INTEGER;
        SUM, MAX, W : INTEGER;

Wie bereits erwähnt wird eine Operation auf allen Elementen eines Arrays mit der For-Anweisung programmiert:

SUM:= 0;
FOR I:= UG TO OG DO SUM:= SUM + A[I];
WRITELN('Die Summe aller Elemente in A ist', SUM);

Um den größten Wert in einem Array zu finden, bestimmt man schrittweise das Maximum der ersten I Zahlen, indem man den bis dahin größten Wert (der I-1 letzten Zahlen) mit dem Element A[I] vergleicht:

MAX:= A[UG];
FOR I:= UG+1 TO OG DO
  IF A[I]>MAX THEN MAX:= A[I];
WRITELN('Die größte Zahl ist', MAX);

Selbst wenn UG = OG ist, arbeitet dieses Programmstück korrekt, da dann die For-Schleife (als pre check loop) wegen UG+1>OG nicht ausgeführt wird. Mit diesem Suchalgorithmus kann man auch ein Array sortieren: Man bestimmt das Maximum des Arrays und vertauscht es mit dem letzten Element im Array. Anschließend wiederholt man diese Prozedur für alle Elemente ohne das Maximum und erhält dadurch den zweitkleinsten Wert. Wiederholt man dieses Verfahren bis zum kleinsten Element des Arrays, so ist das Feld anschließend aufsteigend sortiert:

FOR J:= OG DOWNTO UG+1 DO
  BEGIN
    (* BESTIMME K, DEN INDEX DES MAXIMUMS *)
    (* IM TEILARRAY A[UG..J].             *)
    (* VERTAUSCHE A[J] MIT A[K]           *)
  END;

Die in Kommentarklammern angegebenen Operationen wurden bereits früher besprochen (s.o.), so daß man diese Programmteile zwischen BEGIN und END unverändert einsetzen kann:

PROGRAM FELDER (INPUT,OUTPUT);
  CONST UG =  1;    (* untere Grenze *)
        OG = 10;    (* obere Grenze  *)
  VAR   I, J, K     : INTEGER;
        A           : ARRAY [UG..OG] OF INTEGER;
        MAX         : INTEGER;
BEGIN
  WRITELN('Unsortierte Folge:');
  (* A zufällig vorbelegen: *)
  FOR I:= UG TO OG DO
    BEGIN 
      A[I]:= INT(RANDOM(0) * 100); WRITE(A[I])
    END;
  WRITELN;
 
  FOR J:= OG DOWNTO UG+1 DO
    BEGIN
      MAX:= A[UG]; K:= UG;
      FOR I:= UG+1 TO J DO
        IF A[I]>MAX THEN
          BEGIN K:=I; MAX:= A[I] END;
      A[K]:= A[J]; A[J]:= MAX
    END;
 
  WRITELN('Sortierte Folge:');
  FOR I:= UG TO OG DO WRITE(A[I]);
  WRITELN;
END.

Ist Ihnen die genaue Funktion dieses Programmes noch nicht ganz klar geworden, sollten Sie mit Stift und Papier das Array mit den Werten

8   9   1   3   4   2   5

nach dem angegebenen Algorithmus sortieren. Dann werden Sie auch verstehen, warum diese Sortiermethode Sortieren durch Auswahl heißt. In Abschnitt 2.11.5 werden Sie ein anderes Sortierverfahren kennenlernen, das für große Arrays wesentlich effizienter ist. In jedem Durchlauf der äußeren Schleife (FOR J:= ...) wird eine Zahl an ihre korrekte Position gestellt:

8   5   1   3   4   2   9
2   5   1   3   4   8   9 
2   4   1   3   5   8   9
2   3   1   4   5   8   9
2   1   3   4   5   8   9
1   2   3   4   5   8   9

Eine weitere elementare Operation mit Arrays besteht darin, einen vorgegebenen Wert im Array zu suchen. Das Ergebnis der Suche soll der Index des Wertes im Array sein. Das Prinzip besteht darin, mit einer Variablen (I) schrittweise das Array zu durchlaufen und das Element A[I] mit dem gesuchten Wert W zu vergleichen, bis eine Übereinstimmung eintritt, oder das Ende des Arrays erreicht wird. Offensichtlich ist hier die For-Anweisung ungeeignet, da nicht a priori die Grenzen für die Laufvariable bekannt sind.

Ein erster Lösungsansatz wäre folgende Schleife:

PROGRAM SUCHE (INPUT,OUTPUT);
(*$R+   Bereichsüberprüfung einschalten! *)
  CONST UG =  1;    (* untere Grenze *)
        OG = 10;    (* obere Grenze  *)
  VAR   I           : INTEGER;
        A           : ARRAY [UG..OG] OF INTEGER;
        W           : INTEGER;
BEGIN
  WRITELN('Zufällige Folge:');
  FOR I:= UG TO OG DO
    BEGIN 
      A[I]:= INT(RANDOM(0) * 100); WRITE(A[I])
    END;
  WRITELN;
 
  WRITE('Suchwert:'); READLN(W);
  I:= UG;
  WHILE (I<=OG) AND (A[I]<>W) DO I:= I+1;
  IF I>OG THEN
    WRITELN(W, ' nicht gefunden')
  ELSE
    WRITELN(W, ' hat den Index ',I);
END.

Jedoch bewirkt diese Schleife einen Zugriff auf das nicht existierende Element A[OG+1], falls der gesuchte Wert W nicht im Array A enthalten ist: Für alle Elemente des Arrays liefert der Vergleich A[I]<>W den Wert TRUE, so daß I im letzten Durchlauf den Wert OG+1 annimmt. Anschließend wird wiederum die Bedingung der While-Anweisung ausgewertet. Zwar ist bereits das Ergebnis des ersten Teilausdruckes (I<=OG) FALSE, dennoch wird in Pascal ein boolescher Ausdruck immer vollständig ausgewertet. Deshalb wird bei der Berechnung des zweiten Teilausdruckes (A[I]<>W) auf das nicht existierende Element A[OG+1] zugegriffen.

Dieser verbotene Zugriff wird normalerweise in Pascal 2.0 nicht erkannt, da Indexausdrücke nicht auf die Grenzen der Deklaration überprüft werden. Der Kommentar (*$R+ *) schaltet jedoch eine Option des Compilers ein, die unter anderem die Indexgrenzen bei jedem Array-Zugriff prüft, so daß beim Programmablauf eine Fehler- meldung erzeugt wird:

VALUE OUT OF BOUNDS: 11  1  10
  ERROR AT xxxx IN SUCHE

Das heißt, es wurde versucht, das 11. Element anzusprechen, obwohl in der Deklaration 1 und 10 als Indexgrenzen vereinbart wurden. Nähres zur Option (*$R+ *) und zur Interpretation von Laufzeitfehlermeldungen finden Sie in Kapitel 4.

Die obige Suche muß also umformuliert werden:

I:= UG-1;
REPEAT
  I:= I+1
UNTIL (A[I]=W) OR (I=OG);

PROGRAM SUCHE (INPUT,OUTPUT);
(*$R+   Bereichsüberprüfung einschalten! *)
  CONST UG =  1;    (* untere Grenze *)
        OG = 10;    (* obere Grenze  *)
        OG1= 11;    (* Feldgröße mit Marke am Ende *)
  VAR   I           : INTEGER;
        A           : ARRAY [UG..OG1] OF INTEGER;
        W           : INTEGER;
BEGIN
  WRITELN('Zufällige Folge:');
  FOR I:= UG TO OG DO
    BEGIN 
      A[I]:= INT(RANDOM(0) * 100); WRITE(A[I])
    END;
  WRITELN;
 
  WRITE('Suchwert:'); READLN(W);
  I:= UG; A[OG1]:=W;                 (* Marke speichern *)
  WHILE A[I]<>W DO I:= I+1;
  IF I=OG1 THEN
    WRITELN(W, ' nicht gefunden')
  ELSE
    WRITELN(W, ' hat den Index ',I);
END.

Mit diesem Programm endet die Behandlung der Algorithmen auf Arrays. Sicher werden Sie den einen oder anderen Hinweis für eigene Pascalprogramme verwenden können. Jeder Leser, der nicht jedes Mal das Rad neu erfinden will, sei auf die Standardliteratur zum Thema Strukturierte Programmierung verwiesen (s. Anhang E). Besonders nützlich ist das Buch [2], in dem alle Algorithmen in Form von Pascal-Quelltexten vorgestellt und ausführlich hergeleitet werden.

Bisher wurden nur einzelne Elemente eines Arrays verändert. Möchte man z.B. den Inhalt des Feldes A in ein Feld B desselben Typs übertragen, so könnte dies wie folgt geschehen:

FOR I:= UG TO OG DO B[I]:= A[I]

In Pascal geht dies aber auch eleganter (und wesentlich schneller) mit der Zuweisung B:=A. Voraussetzung hierfür ist, daß A und B denselben Typ besitzen. Wann zwei zusammengesetzte Variablen zuweisungskompatibel sind, wird im Abschnitt 2.10 genau erklärt.

PROGRAM ARRAYSLICES (INPUT,OUTPUT);
  CONST UG =  1;    (* untere Grenze *)
        OG = 10;    (* obere Grenze  *)
  VAR   I           : INTEGER;
        A,B         : ARRAY [UG..OG] OF INTEGER;
BEGIN
  WRITELN('Zufällige Folge:');
  FOR I:= UG TO OG DO A[I]:= INT(RANDOM(0) * 100);
  B:=A;
  FOR I:= UG TO OG DO
    WRITELN(A[I]:8, B[I]:8);
END.

Inhaltsverzeichnis